Cara Menggunakan Mail Merge di Microsoft Word 2007

Microsoft Word merupakan program yang memang didesain untuk mengerjakan dan membuat dkumen/file berpat text.  Pada umumnya Word digunakan untuk membuat surat-surat perkantora.  Jaman semakin maju saat ini dengan menggunakan MS. Word anda dapat membuat surat dengan alamat yang berbeda dengan jumlah yang banya dan dapat menyelesaikannya dengan cepat.
Ms. Word sudah ada tools tersendiri untuk melakukan hal tersebut.  Tools tersebut sudah saya lakukan dan diulas pada tulisan berjudul membuat label undangan.  Tools tersebut bernama Mail Merge, nah bagaimana cara menggunakannya?  Mari kita belajar bersama-sama menggunakan Mail Merge.
Contoh latihannya misalnya kita akan membuat surat undangan reunian.  Tentunya surat undangan tersebut harus disebar ke peserta reunian yang jumlahnya ratusan orang.  Tentunya akan menyulitkan kita sendiri jika kita menulis nama dan alamat penerima surat undangannya dengan tulisan tangan atau mengetik satu per satu.  Nah untuk mempercepat pekerjaan ini kita bisa gunakan Mail Merge.

Langkah – langkah Penggunaan Mail Merge pada Surat Undangan

1. Langkah pertama yaitu anda harus membuat file data base list daftar nama dan alamat yang diundang pada file Microsoft Excel.  Contohnya seperti ini:

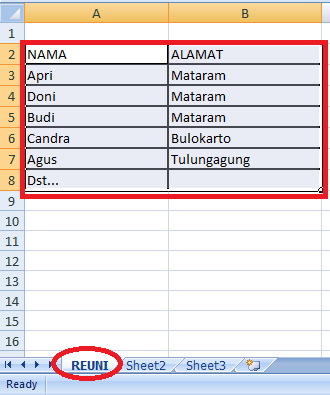
Beri nama Sheet dengan REUNI atau terserah anda memberikan nama apa saja.  Simpan file Excel tersebut dengan nama Data Base Reuni.
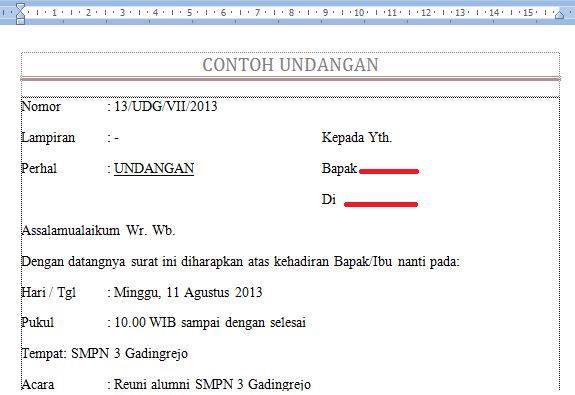
2. Sekarang buka file undangan di Ms. Word 2007 anda.  Perhatikan untuk nama dan alamat penerima undangan dikosongkan dahulu karena nantinya kita akan isi dengan langkah mail merge.

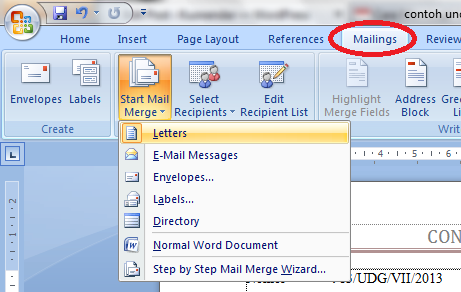
3. Oke, sekarang saatnya kita beraksi.  Letakkan kursor anda pada bagian setelah kata Bapak.  Lalu pilih menu Mailings>>Start Mail Merge>>Letters.

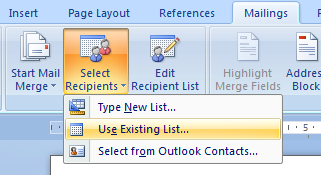
4. Setelah itu pilih menu Select Recipients>>Use Existing List.

5. Lalu pilih data base reuni yang sudah kita buat tadi di excel.

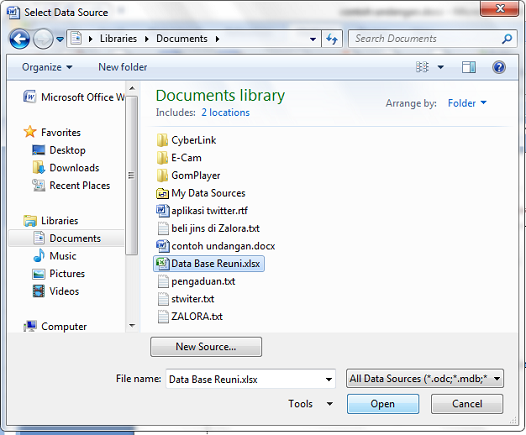6. Karena tadi kita membuat data base-nya di Sheet REUNI pilih aja yang pertama, lalu OK.

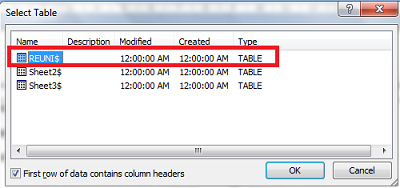
7. Lalu pilih menu Edit Recipients List untuk sekedar mengecek data base saja.  Perhatikan!! biasanya pada NAMA dan ALAMAT berupa tulisa F1 dan F2.  Lalu OK.

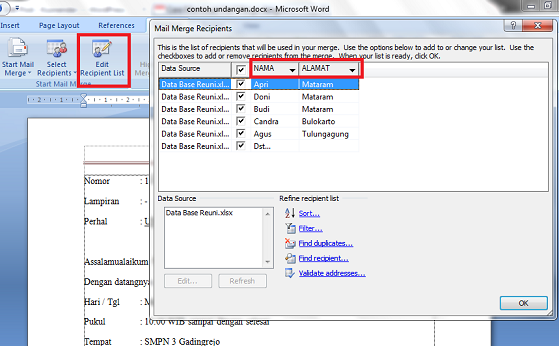8. Selanjutnya pastikan kursor anda tepat di belakang tulisan BAPAK.  selanjutnya pilih menu Insert Merge Field>>Nama. dan Insert Merge Field>>Alamat di belakang kata “DI”.

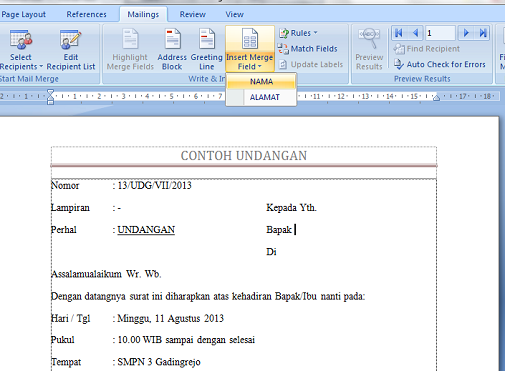Nantinya jadinya seperti ini.

9.  Tahap terakhir yaitu pilih menu Finish & Merge >> Edit Individual Documents untuk melihat dokumennya atau Print Documents secara langsung surat akan tercetak dengan nama dan alamat yang berbeda.

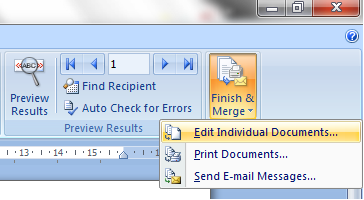
10.  Jika anda memilih yang Edit Individual pilih ALL.

Maka file word akan membuat file baru dengan surat undangan yang sudah terisi nama dan alamat penerima surat undangan.
Sangat mudah sekali kan menggunakan mail merge di Microsoft Word 2007.  Dengan begini anda dapat membuat surat undangan dengan nama dan alamat penerima undangan banyak dalam waktu yang singkat.

Keindahan Belajar Matematika

 Matematika dalam Islam

18 Oktober 2013 pukul 10:54

Mudah”ah ini jadi motivasi buat kita agar tidak ketergantungan menggunakan kalkulator dalam perhitungan yang sederhana…. #asah_otak_kita
Mari berhitung ..hehe
1 x 8 + 1 = 9 12 x 8 + 2 = 98 123 x 8 + 3 = 987 1234 x 8 + 4 = 9876 12345 x 8 + 5 = 98765 123456 x 8 + 6 = 987654 1234567 x 8 + 7 = 9876543 12345678 x 8 + 8 = 98765432 123456789 x 8 + 9 =  987654321
1 x 9 + 2 = 11 12 x 9 + 3 = 111 123 x 9 + 4 = 1111 1234 x 9 + 5 = 11111 12345 x 9 + 6 = 111111 123456 x 9 + 7 = 1111111 1234567 x 9 + 8 = 11111111 12345678 x 9 + 9 = 111111111 123456789 x 9 +10= 1111111111
9 x 9 + 7 = 88 98 x 9 + 6 = 888 987 x 9 + 5 = 8888 9876 x 9 + 4 = 88888 98765 x 9 + 3 = 888888 987654 x 9 + 2 = 8888888 9876543 x 9 + 1 = 88888888 98765432 x 9 + 0 = 888888888
1 x 1 = 1 11 x 11 = 121 111 x 111 = 12321 1111 x 1111 = 1234321 11111 x 11111 = 123454321 111111 x 111111 = 12345654321 1111111 x 1111111 = 1234567654321 11111111 x 11111111 = 123456787654321 111111111 x 111111111 = 12345678987654321
Nah sekarang saatnya kita membaca artikel yang akan saya share di sini mengenai MATEMATIKA dalam ISLAM. . . .  Keajaiban Islam dalam ilmu pengetahuan!!!
TANGGAL 17 bulan Ramadan kemarin diperingati sebagai malam turunnya Alquran. Alquran merupakan mukjizat terbesar yang diturunkan Allah SWT kepada Nabi Muhammad saw. Sudah banyak bukti yang menerangkan kemukjizatan Alquran, baik dari segi tata bahasa maupun isinya. Pada bagian ini penulis hendak menyoroti kemukjizatan Al-quran dari segi matematika. Di sebagian benak kita, sudah dianggap umum agama ” itu tidak ada hubungannya dengan masalah iptek. Padahal, jika dicermati lebih jauh, Alquran memuat segala sesuatu. Dalam firmannya Allah SWT menyatakan tidak ada sesuatu apa pun yang aku tinggalkan dalam Alquran. Hal ini berlaku juga dengan ilmu matematika. Anggapan kita matematika itu tidak ada hubungan sama sekali dengan Alquran. Apakah anggapan ini benar? Jika kita cermati, banyak surat dalam Alquran yang berbicara mengenai matematika. Dalam Alquran ada matematika yang dibahas secara tersurat. Contohnya, masalah pecahan disebutkan dalam surat Annisa. Dalam surat ini bilangan pecahan secara eksplisit disebutkan dalam hal pembagian warisan. Masalah waktu juga menjadi hal yang paling sering dibahas dalam Alquran. Secara tersirat Alquran pun menunjukkan matematika yang mencengangkan. Seorang peneliti Muslim Dr. Tariq Al-Suwaidan menemukan data menakjubkan tentang Alquran. Salah satunya, ia menemukan fakta banyak kata Al-Bahar (Lautan) ada 32 dan kata Al-Bar (Daratan) ada 13. Jika banyak kata ini dibagi dengan banyak dua kata tersebut diperoleh = 71,2% dan = 28,8%. Fakta ini sama dengan pengetahuan masa kini yang menyatakan luas lautan adalah 71,2 % dan luas daratan 28,8%. Dr. Tariq Al-Suwaidan juga menemukan data tentang keteraturan dari kata yang ada dalam Alquran. Banyak kata yang berlawanan dalam Alquran adalah sama. Contohnya, Kata Ad-Dunya (dunia) banyaknya ada 115, sama dengan banyak lawan dari kata tersebut, yaitu Al-Akhira (akhirat).
Nisbah emas
Dalam salah satu ayatnya, Allah SWT menerangkan Allah menciptakan segala sesuatu dengan perhitungan yang sangat cermat. Ingin mengetahui salah satu bukti dari ayat ini? Uraian berikut menunjukkan kebenaran ayat ini. Coba ukur tinggi badan dan tinggi dari bahu sampai ujung kaki. Berapakah perbandingan antara tinggi badan dan tinggi dari bahu sampai ujung kaki? Sekarang, ukur lagi panjang tangan. Ukur pula panjang dari siku sampai ujung tangan. Berapakah perbandingannya? Jika teliti, akan ditemukan perbandingan dua kasus ini sama, yaitu 1,618: 1. Subhanalloh maha besar Allah yang telah membuat ciptaannya dengan perhitungan yang akurat. Perbandingan seperti ini disebut nisbah emas. Nisbah emas ini juga dapat ditemukan di alam, seperti kelopak bunga dan cangkang kerang. Perbandingan ini merupakan perbandingan yang paling enak untuk dipandang mata. Para seniman dan arsitek telah lama menggunakan nisbah ini dalam membangun sebuah bangunan. Contohnya, perbandingan panjang alas piramida Gizeh dan tingginya menganut nisbah ini. Malahan, pelukis terkenal Leonardo Da Vinci selalu menggunakan perbandingan ini dalam setiap karyanya. Pada lukisan Monalisa, perbandingan antara daerah di kanan dan kiri wajah menganut perbandingan ini.
Matematika island
Sejak 1997 negara kita telah dilanda krisis ekonomi hingga saat ini. Salah satu hal penting yang menyebabkan terjadinya krisis ini adalah krisis moral. Korupsi dan nepotisme telah menjadi hal yang biasa. Untuk mengatasi krisis moral ini bukanlah perkara yang mudah. Semua pihak yang terkait harus berusaha semaksimal mungkin untuk memperbaiki kualitas moral bangsa ini. Salah satu upaya yang penting adalah melalui pendidikan di sekolah. Akan tetapi, yang menjadi masalah adalah masih adanya jurang pemisah yang sangat lebar antara pelajaran dan moral (agama). Di benak kebanyakan siswa, ada anggapan ilmu pengetahuan dan agama itu sesuatu yang sangat terpisah. Ilmu pengetahuan tidak ada hubungannya dengan masalah agama. Begitu juga dengan agama yang tidak berhubungan dengan ilmu pengetahuan. Terlebih Lagi dengan pelajaran matematika dan Islam itu sangat erat hubungannya. Faktanya, sejumlah surat dalam Alquran mengandung matematika. Beberapa penelitian matematika sekarang membuktikan kebenaran Al-quran. Untuk menepis anggapan seperti ini, perlu diberikan pembelajaran matematika yang memadukan antara matematika dan agama. Pembelajaran seperti ini sangat cocok diajarkan di SDIT, SMPIT, dan SMATT. Bagaimana cara mengajarkan matematika yang islami. Ada beberapa cara yang dapat dilakukan. Hal yang pertama adalah menggunakan masalah konteks agama untuk memulai menerangkan matematika. Masalahnya bisa berupa manfaat yang diperoleh siswa yang berkaitan dengan masalah agama. Contohnya untuk mempelajari pecahan, siswa diajak untuk melihat masalah waris dalam surat Annisa. Dalam surat ini tertera dengan jelas mengenai pentingnya menguasai masalah perhitungan dengan pecahan. Selain itu, masalah pecahan pun diperlukan dalam perhitungan zakat. Contoh lainnya dalam mengenalkan aturan operasi hitung campuran. Aturan ini berisi urutan mengerjakan soal yang ada beberapa operasi hitung. Biasanya aturan ini langsung diberikan kepada siswa tanpa diberi makna atau manfaatnya. Ada baiknya jika aturan ini dijelaskan dengan cara menganalogikan dengan cara berpakaian. Menurut sebuah hadis, pada saat berpakaian kita dianjurkan mendahulukan bagian kanan daripada bagian kiri. Aturan seperti ini merupakan aturan yang sudah diterima dan dilakukan oleh kita semua. Dalam matematika, aturan yang seperti ini juga ada. Aturan inilah yang disebut urutan pengerjaan hitung campuran. Masih banyak lagi masalah konteks agama yang dapat dijadikan sebagai pemantik untuk mempelajari matematika. Cara kedua memberikan fakta-fakta yang menunjukkan kebesaran Allah SWT. Contohnya Cheetah termasuk binatang ciptaan Allah yang kecepatan larinya tercepat. Kecepatan larinya bisa mencapai 102 km/jam. Walaupun demikian, manusia telah dianugerahi Tuhan otak untuk berpikir. Manusia dapat membuat kendaraan yang kecepatannya melebihi kecepatan Cheetah, seperti mobil dan pesawat terbang. Subhanalloh, mahabesar Allah yang telah menganugerahi kita otak untuk berpikir. Sungguhlah benar firmannya: manusia itu diciptakan dalam keadaan yang sempurna. Cara ketiga memberikan cerita matematika yang menggugah siswa. Cerita berikut dapat dijadikan acuan. Matematika Membuktikan: Bekerjasama Lebih Menguntungkan Daud akan membagikan tanahnya seluas 40.000 m2 pada dua pegawainya yang saling membenci, Firman dan Yusuf. Daud berpikir bahwa manusia bersifat serakah. Oleh karena itu, pembagian yang macam apa pun, pasti dianggap tidak adil. Sebaliknya, kalau dibiarkan mereka yang membagi tanah itu, pasti mereka akan saling membunuh. Cara terbaik membiarkan keserakahan itu berjalan dan mereka lihat apa hasilnya, pikir Daud. Daud memanggil kedua pegawainya dan memberikan masing- masing seutas tali yang panjangnya 400 m. “Kalian mendapatkan tanah seluas yang dapat kalian batasi dengan tali-tali tersebut,” kata Daud. Firman dan Yusuf segera pergi bersemangat dan berpacu membentangkan tali mengelilingi tanah itu seluas mungkin sebagai batas miliknya. Hasilnya diperlihatkan pada Gambar 1. Ternyata, Firman berhasil membentangkan tali itu membentuk sebidang tanah dengan luas 120 m” 80 m = 9.600 m2. Adapun Yusuf berhasil mendapatkan 40 m” 160 m = 6.400 m2. Total luas tanah mereka adalah 16.000 m2. Padahal, luas tanah yang tersedia 40.000 m2. Sementara itu, Firman mendapat tanah yang lebih luas dan Yusuf menyesali kebodohannya. “Kembalilah!” kata Daud ketika keduanya menghadap. “Bentangkan tali itu sekali lagi supaya kalian bisa mendapatkan lebih banyak. Jangan merasa terlalu cepat puas,” kata Daud. Mereka pun kembali. Setelah mencoba-coba merentangkan tali-tali itu dengan berbagai cara, mereka menyadari bahwa luas tanah maksimum yang mungkin mereka peroleh adalah jika panjang tanah sama dengan lebar tanah.Oleh karena panjang tali yang 400 m itu merupakan keliling tanah, maka panjang dai lebar tanah yang memberikan luas maksimum adalah 100 m Jadi, masing-masing memperoleh tanah seluas 100 m x 100 m = 10.000 m2. Luas tanah keduanya menjadi 20.000 m2 Padahal, tanah yang akan diberikan 40.000 m2, berarti ada sisa 20.000 m2 lagi. Daud berkata, kembalilah ke tanah itu. Bentangkan tali itu sekali lagi karena kalian bisa mendapat lebih banyak lagi. Firman dan Yusuf menjelaskan bahwa menurut hukum matematika tidak mungkin mendapat tanah yang lebih luas dari 10.000 m2. Ya, kata Daud. Akan tetapi, kalian melupakan hukum matematika yang lain. Kembalilah kalian pasti bisa mendapatkan lebih banyak. Kata Baud. Bagaimana mungkin? Setelah berpikir beberapa saat, Firman dan Yusuf tiba-tiba menyadari kedunguan mereka. Keserakahan telah menutupi hati mereka. Sebenarnya, mereka bisa mendapatkan tanah yang lebih luas jika keduanya berjabatan tangan bekerja sama. Caranya kedua tali ini disambungkan sehingga panjangnya menjadi 800 m. Dengan begitu, panjang dan lebar tanah yang memberi luas maksimal adalah 200 m. Dengan ukuran ini, luas tanah yang diperoleh menjadi 200 m x 200 m = 40.000 m2. Firman dan Yusuf berpelukan. Kini mereka mendapat tanah yang lebih luas, masing-masing 20.000 m2.
Takhayul
Dalam kehidupan sehari-hari, kita sering mendengar hal-hal yang tidak masuk akal. Misalnya, jika ada suara burung uncuing, itu tandanya akan ada yang meninggal. Mengapa masalah takhayul itu dilarang agama? Uraian berikut merupakan salah satu penjelasan mengapa hal tersebut dilarang. Di dalam psikologi ada yang dinamakan dengan falacy of dramatic instan. Keadaan ini merupakan suatu kesalahan dalam proses berpikir, seseorang terlalu cepat menyimpulkan sesuatu. Dengan melihat beberapa polanya, seseorang yang mengidap keadaan ini cepat menyimpulkan. Proses terjadinya takhayul ini mirip dengan keadaan ini. Suatu takhayul dijadikan suatu kebenaran karena seseorang mengalami hal ini, beberapa kali, lalu menyimpulkannya. Dalam matematika kita mengenal suatu prinsip yang dinamakan induksi matematika. Prinsip ini digunakan untuk membuktikan suatu rumus atau aturan berlaku secara umum. Dengan prinsip ini, suatu aturan tidak bisa sekaligus berlaku secara umum. Ada beberapa tahapan yang diperlukan agar rumus ini berlaku secara umum. Dengan begitu, orang yang mengetahui prinsip ini akan berhati-hati dalam menyimpulkan sesuatu. Masalah takhayul yang masih banyak terjadi di masyarakat mungkin takkan terjadi jika setiap orang memahami prinsip ini. Pernahkah membaca ramalan bintang di majalah? Atau pernahkah menonton paranormal yang meramalkan masa depan? Ketika kita membaca ramalan bintang, kadang ada beberapa bagian dari ramalan si peramal yang isinya persis sama seperti yang kita alami. Dengan adanya beberapa bagian yang isinya mirip dengan apa yang terjadi pada kita, lantas kita percaya pada ramalan tersebut. Padahal, hal ini dapat merusak iman kita. Dengan jelas Alquran melarang hal tersebut karena sudah masuk dalam kemusyrikan. Mengapa peramal tersebut dapat meramalkan beberapa bagian yang benar? Mengapa hal ini bisa terjadi? Padahal, kita tahu yang membuat ramalan bintang itu manusia. Ia bukanlah Tuhan yang tahu apa yang terjadi di masa depan. Untuk mengetahui jawaban ini, kita akan menganalisisnya dengan menggunakan prinsip yang ada dalam matematika. Dalam matematika ada suatu prinsip yang dikenal dengan prinsip burung merpati (pigeon hole principal). Prinsip ini menyatakan jika ada 3 sarang dan 4 burung merpati, pasti ada satu sarang yang berisi lebih dari 1 merpati. Misalkan, kita analogikan manusia dengan merpati serta keadaan yang akan terjadi pada manusia (takdir) dengan sarangnya. Tentu saja manusia akan lebih banyak daripada takdirnya. Misalnya, kita anggap ada 100 juta orang dewasa di Indonesia. Adapun takdirnya mengenai masalah kesehatan hanya ada tiga kemungkinan, yaitu sehat, kurang sehat, dan sakit. Oleh karena manusianya (merpati) ada 100 juta, sedangkan sarangnya, hanya ada 3 tentu saja pasti ada orang yang takdirnya akan sama. Dengan begitu, pasti ada orang yang takdirnya sama. sumber  (Taofik Hidayat, S.Si., Mahasiswa S-2 Matematika ITB)***

rumus statistik

[STATISTIKA] Penyajian Data Ukuran menjadi Data Statistik Deskriptif

0 komentar
Posted in Label: Matematika

undefined
undefined

1. Rataan Hitung (Mean)

Masih ingatkah Anda cara menghitung rataan hitung? Misalnya, seorang guru mencatat hasil ulangan 10 orang siswanya, sebagai berikut.
6 5 5 7 7,5 8 6,5 5,5 6 9
Dari data tersebut, ia dapat menentukan nilai rataan hitung, yaitu

Jadi, nilai rataan hitungnya adalah 6,55.
Secara umum, apabila nilai data kuantitatif tidak dikelompokkan dan dinyatakan oleh x1, x2, …, xn (terdapat n buah datum), nilai rataan hitung (mean) x ditentukan oleh rumus berikut.

Perhitungan nilai rataan hitung akan menjadi lain jika guru tersebut mencatat hasil ulangan 40 orang siswanya sebagai berikut:
3 orang mendapat nilai 4
4 orang mendapat nilai 5
6 orang mendapat nilai 5,5
8 orang mendapat nilai 6
7 orang mendapat nilai 7
10 orang mendapat nilai 8
2 orang mendapat nilai 9
Nilai rataan hitung siswa dapat dicari sebagai berikut:

Jadi, nilai rataan hitungnya adalah 6,5.
Secara umum, apabila nilai-nilai data kuantitatif dinyatakan dengan x1, x2, …, xn (terdapat n buah datum) dengan setiap nilai datum mempunyai frekuensi f 1 , f 2 , …, f n maka rataan hitung ( x ) ditentukan oleh rumus berikut.

Contoh soal:
1. Seorang peneliti mencatat banyak bayi yang lahir selama setahun di 20 kecamatan. Hasil pencatatannya disajikan berikut.
136 140 220193 130 158 242 127 184 213
200 131 111 160 217 281 242 242 281 192
a. Hitunglah rataan hitung (mean) data tersebut.
b. Tentukan jangkauan datanya.
c. Tentukanlah jangkauan antarkuartil.
2. Nilai rataan hitung (rata-rata) ujian matematika dari 38 orang siswa adalah 51. Jika nilai dari seorang siswa lain yang bernama Rahman digabungkan dengan kelompok itu maka nilai rataan hitung ujian matematika dari 39 orang siswa sekarang menjadi 52. Tentukanlah nilai yang diperoleh Rahman.
Jawab :

2. Menghitung Rataan Hitung dengan Menggunakan Rataan Hitung Sementara
Rataan hitung dapat pula ditentukan dengan menggunakan rataan hitung sementara (xs). Untuk kumpulan data berukuran besar, biasanya rataan hitung ditentukan dengan menggunakan rataan hitung.
Langkah pertama dalam menentukan rataan hitung dengan menggunakan rataan hitung sementara adalah menentukan rataan sementara dari nilai tengah salah satu kelas interval. Kemudian, semua nilai tengah pada setiap kelas interval dikurangi rataan hitung sementara tersebut.
Setiap hasil pengurangan tersebut disebut simpangan terhadap rataan hitung sementara itu (di). Adapun rumus untuk mencari rataan hitung sementara adalah sebagai berikut.

Contoh soal:

Tabel 1.11 menunjukkan hasil ulangan Fisika dari 71 siswa Kelas XI SMA Merdeka. Tentukanlah rataan hitung dengan menggunakan rataan hitung sementara.
Jawab :

3. Modus, Median, Kuartil, dan Desil

a. Modus (Mo)
Seorang guru ingin mengetahui nilai manakah yang paling banyak diperoleh siswanya dari data hasil ulangan matematika. Tentunya, ia akan menentukan datum yang paling sering muncul. Misalnya, data hasil ulangan 10 orang siswa sebagai berikut
7 4 6 5 7 8 5,5 7 6 7
Data yang paling sering muncul disebut modus. Modus dari data itu adalah 7 sebab nilai yang paling sering muncul adalah 7. Modus mungkin tidak ada atau jika ada modus tidak tunggal.
Jika data yang diperoleh berukuran besar, data perlu dikelompokkan agar penentuan modus mudah dilakukan. Modus dari data yang dikelompokkan dapat dicari dengan menggunakan rumus berikut.

dengan
L = batas bawah nyata (tepi bawah) dari kelas modus
d1 = selisih antara frekuensi dari kelas yang mengandung modus dan frekuensi dari kelas yang mendahuluinya (sebelumnya).
d 2 = selisih antara frekuensi dari kelas yang mengandung modus dan frekuensi dari kelas berikutnya
i = interval kelas/panjang kelas.
Telah Anda ketahui modus adalah datum yang paling sering muncul. Prinsip ini digunakan untuk menentukan kelas modus pada data yang dikelompokkan. Kelas modus adalah kelas yang frekuensinya paling banyak.
Contoh soal:
1. Tentukan modus dari data berikut ini.
a. 45, 50, 50, 64, 69, 70, 70, 70, 75, 80
b. 50, 65, 65, 66, 68, 73, 73, 90
c. 35, 42, 48, 50, 52, 55, 60

2. Tabel menunjukkan hasil ulangan matematika dari 71 siswa Kelas XI SMA Bhinneka. Tentukan modus dari data tersebut.
Jawab :

b. Median dan Kuartil
Dari data kuantitatif yang tidak dikelompokkan dan dinyatakan oleh x1, x2, …, xn, (dengan x1 < x2 < … < xn) untuk n yang berukuran besar (yang dimaksud n berukuran besar yaitu n = 30) maka nilai ketiga kuartil, yaitu Q1 (kuartil bawah),Q2 (median), dan Q3 (kuartil atas) ditentukan dengan rumus berikut.

Contoh soal :
Tentukan median, kuartil bawah, dan kuartil atas dari databerikut.
67 86 77 92 75 70
63 79 89 72 83 74
75 103 81 95 72 63
66 78 88 87 85 67
72 96 78 93 82 71
Jawab :

Untuk data yang dikelompokkan, nilai median (Me) dan kuartil (Q) ditentukan dengan rumus sebagai berikut.

Contoh soal:

Tentukan median, kuartil bawah, dan kuartil atas dari data pada Tabel di atas.
Jawab :

c. Desil
Untuk data sebanyak n dengan n ≥ 10, Anda dapat membagi data tersebut menjadi 10 kelompok yang memuat data sama banyak. Ukuran statistik yang membagi data (setelah diurutkan dari terkecil) menjadi 10 kelompok sama banyak disebut desil. Sebelum data dibagi oleh desil, data harus diurutkan dari yang terkecil.
Oleh karena data dibagi menjadi 10 kelompok sama banyak maka didapat 9 desil. Amati pembagian berikut.

Terdapat 9 buah desil, yaitu desil pertama(D1), desil kedua (D2), ..., desil kesembilan (D9).
Letak desil ditentukan dengan rumus berikut.

Dalam hal ini i = 1, 2, 3, ..., 9 dan n = banyak data.
Contoh soal:
Tentukan desil ke-1 dan desil ke-5 dari data berikut.
47, 33, 41, 37, 46, 43, 39, 36, 35, 42, 40, 39, 45
Jawab :

Untuk data yang disusun dalam daftar distribusi frekuensi, nilai desil ditentukan sebagai berikut.

Dalam hal ini i = 1, 2, 3, ..., 9
(t b )Di = tepi bawah kelas Di
Fi = frekuensi kumulatif sebelum kelas Di
f i = frekuensi kelas Di
p = panjang kelas
Contoh soal:
Tentukan nilai desil ketiga dari data pada Tabel

Jawab :

4. Simpangan Rata-Rata, Ragam, dan Simpangan Baku


a. Simpangan Rata-Rata
Sekumpulan data kuantitatif yang tidak dikelompokkan dinyatakan oleh x1, x2, …, xn. Dari data tersebut dapat ditentukan simpangan rata-rata (SR) dengan menggunakan rumus:

Contoh soal:
Hitung simpangan rata-rata dari data kuantitatif berikut:
12, 3, 11, 3, 4, 7, 5, 11
Jawab :

Untuk sekumpulan data yang dinyatakan oleh x1, x2, …, xn dan masing-masing nilai data tersebut mempunyai frekuensi f 1 , f 2 , …, f n diperoleh nilai simpangan rata-rata (SR) dengan menggunakan rumus:

Contoh soal:
Hitunglah simpangan rata-rata nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka seperti Tabel

Jawab :

b. Simpangan Baku
Diketahui sekumpulan data kuantitatif yang tidak dikelompokkan dan dinyatakan oleh x1, x2, …, xn. Dari data tersebut, dapat diperoleh nilai simpangan baku (S) yang ditentukan oleh rumus berikut

Contoh soal:
Dari 40 orang siswa diambil sampel 9 orang untuk diukur tinggi badannya, diperoleh data berikut:
165, 170, 169, 168, 156, 160, 175, 162, 169.
Hitunglah simpangan baku sampel dari data tersebut.
Jawab :

Sekumpulan data kuantitatif yang dikelompokkan, dapat dinyatakan oleh x1, x2, …, xn dan masing-masing data mempunyai frekuensi f 1 , f 2 , …, f n . Simpangan baku (S) dari data tersebut diperoleh dengan menggunakan rumus

Contoh soal:
Hitunglah simpangan baku dari nilai ulangan Fisika dari 71 siswa kelas XI SMA Merdeka sesuai Tabel

Jawab :

c. Variansi (Ragam)
Untuk data yang tidak dikelompokkan ataupun data yang dikelompokkan, diperoleh nilai variansi (v) dengan menggunakan rumus:

Contoh soal:
Hitunglah variansi dari data
Dari 40 orang siswa diambil sampel 9 orang untuk diukur tinggi badannya, diperoleh data berikut:
165, 170, 169, 168, 156, 160, 175, 162, 169.
Jawab :
Dari hasil perhitungan sebelumnya diperoleh S = 5,83 maka
v = S2 = (5,83)2 = 33,99.


d. Koefisien Keragaman (KK)
Rumus koefisien keragaman (KK) dari sekumpulan data x1, x2, x3, ..., xn adalah

Contoh soal:
Pak Murtono seorang pengusaha. Bidang usaha yang ia jalani adalah penerbitan, tekstil, dan angkutan. Dalam 5 bulan terakhir, ia mencatat keuntungan bersih ketiga bidang usahanya. Hasilnya tampak pada Tabel

Jika Pak Murtono berpendapat bahwa bidang usaha yang akan dipertahankan hanya dua bidang usaha dengan kriteria bidang usaha dengan keuntungan bersih yang stabil, tentukanlah bidang usaha yang sebaiknya tidak dilanjutkan.
Jawab :

sumber : bse matematika